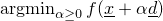- java.lang.Object
-
- de.jstacs.algorithms.optimization.DifferentiableFunction
-
- All Implemented Interfaces:
- Function
- Direct Known Subclasses:
- LogPrior, MEMTools.DualFunction, NegativeDifferentiableFunction, NumericalDifferentiableFunction, OptimizableFunction
public abstract class DifferentiableFunction extends Object implements Function
This class is the framework for any (at least) one time differentiable function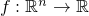 .
.- Author:
- Jens Keilwagen
-
-
Constructor Summary
Constructors Constructor and Description DifferentiableFunction()Default constructor, automatically sets the internal function for line search to aOneDimensionalSubFunctionofthisDifferentiableFunction.
-
Method Summary
All Methods Instance Methods Abstract Methods Concrete Methods Modifier and Type Method and Description abstract double[]evaluateGradientOfFunction(double[] x)Evaluates the gradient of a function at a certain vector (in mathematical sense)x, i.e.,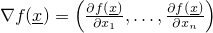 .
.double[]findOneDimensionalMin(double[] x, double[] d, double alpha_0, double fAlpha_0, double linEps, double startDistance)This method is used to find an approximation of an one-dimensional subfunction.-
Methods inherited from class java.lang.Object
clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait
-
Methods inherited from interface de.jstacs.algorithms.optimization.Function
evaluateFunction, getDimensionOfScope
-
-
-
-
Constructor Detail
-
DifferentiableFunction
public DifferentiableFunction()
Default constructor, automatically sets the internal function for line search to aOneDimensionalSubFunctionofthisDifferentiableFunction.
-
-
Method Detail
-
evaluateGradientOfFunction
public abstract double[] evaluateGradientOfFunction(double[] x) throws DimensionException, EvaluationExceptionEvaluates the gradient of a function at a certain vector (in mathematical sense)x, i.e.,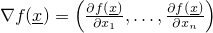 .
.- Parameters:
x- the current vector- Returns:
- the evaluation of the gradient of a function, has dimension
Function.getDimensionOfScope() - Throws:
DimensionException- ifdim(x) != n, with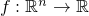
EvaluationException- if there was something wrong during the evaluation of the gradient- See Also:
Function.getDimensionOfScope()
-
findOneDimensionalMin
public double[] findOneDimensionalMin(double[] x, double[] d, double alpha_0, double fAlpha_0, double linEps, double startDistance) throws DimensionException, EvaluationExceptionThis method is used to find an approximation of an one-dimensional subfunction. That means it will find an approximation of the minimum starting at pointxand search in directiond,- Parameters:
x- the start pointd- the search directionalpha_0- the initial alphafAlpha_0- the initial function value (this value is known in most cases and does not have to be computed again)linEps- the tolerance for stopping this methodstartDistance- the initial distance for bracketing the minimum- Returns:
double[2] res = { alpha*, f(alpha*) }- Throws:
DimensionException- if there is something wrong with the dimensionEvaluationException- if there was something wrong during the evaluation of the function- See Also:
OneDimensionalFunction.findMin(double, double, double, double)
-
-